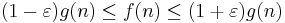Normal order of an arithmetic function
In number theory, the normal order of an arithmetic function is some simpler or better-understood function which "usually" takes the same or closely approximate values.
Let ƒ be a function on the natural numbers. We say that the normal order of ƒ is g if for every ε > 0, the inequalities
hold for almost all n: that is, if the proportion of n ≤ x for which this does not hold tends to 0 as x tends to infinity.
It is conventional to assume that the approximating function g is continuous and monotone.
Contents |
Examples
- The Hardy–Ramanujan theorem: the normal order of ω(n), the number of distinct prime factors of n, is log(log(n));
- The normal order of Ω(n), the number of prime factors of n counted with multiplicity, is log(log(n));
- The normal order of log(d(n)), where d(n) is the number of divisors of n, is log(2) log(log(n)).
See also
References
- G.H. Hardy; S. Ramanujan (1917). "The normal number of prime factors of a number". Quart. J. Math. 48: 76–92. http://www.imsc.res.in/~rao/ramanujan/CamUnivCpapers/Cpaper35/page1.htm.
- G.H. Hardy; E.M. Wright (2008). An Introduction to the Theory of Numbers (6th ed.). Oxford University Press. pp. 473. ISBN 0-19-921986-5.
- Gérald Tenenbaum (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge studies in advanced mathematics. 46. Cambridge University Press. pp. 299–324. ISBN 0-521-41261-7.
External links
- Weisstein, Eric W., "Normal Order" from MathWorld.